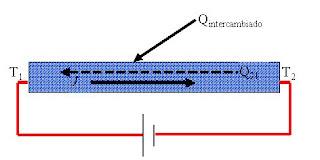
El efecto Thompson consiste en la absorción o liberación de calor por parte de un conductor eléctrico homogéneo, con una distribución de temperaturas no homogénea, por el que circula una corriente.
El flujo neto de potencia calorífica por unidad de volumen, en un conductor de resistividad r, con un gradiente longitudinal de temperatura, por el que circula una densidad de corriente J será:
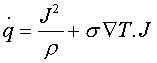donde s es el coeficiente Thompson. El primer término corresponde al efecto Joule, irreversible, mientras que el segundo expresa el efecto Thompson, reversible.Desarrollando esta expresión para obtener la relación entre el coeficiente Thompson y Seebeck y teniendo en cuenta las ecuaciones que rigen los efectos Peltier y Seebeck, se llega a:
Quedando para la unión:
No hay comentarios:
Publicar un comentario